ALGORITHM
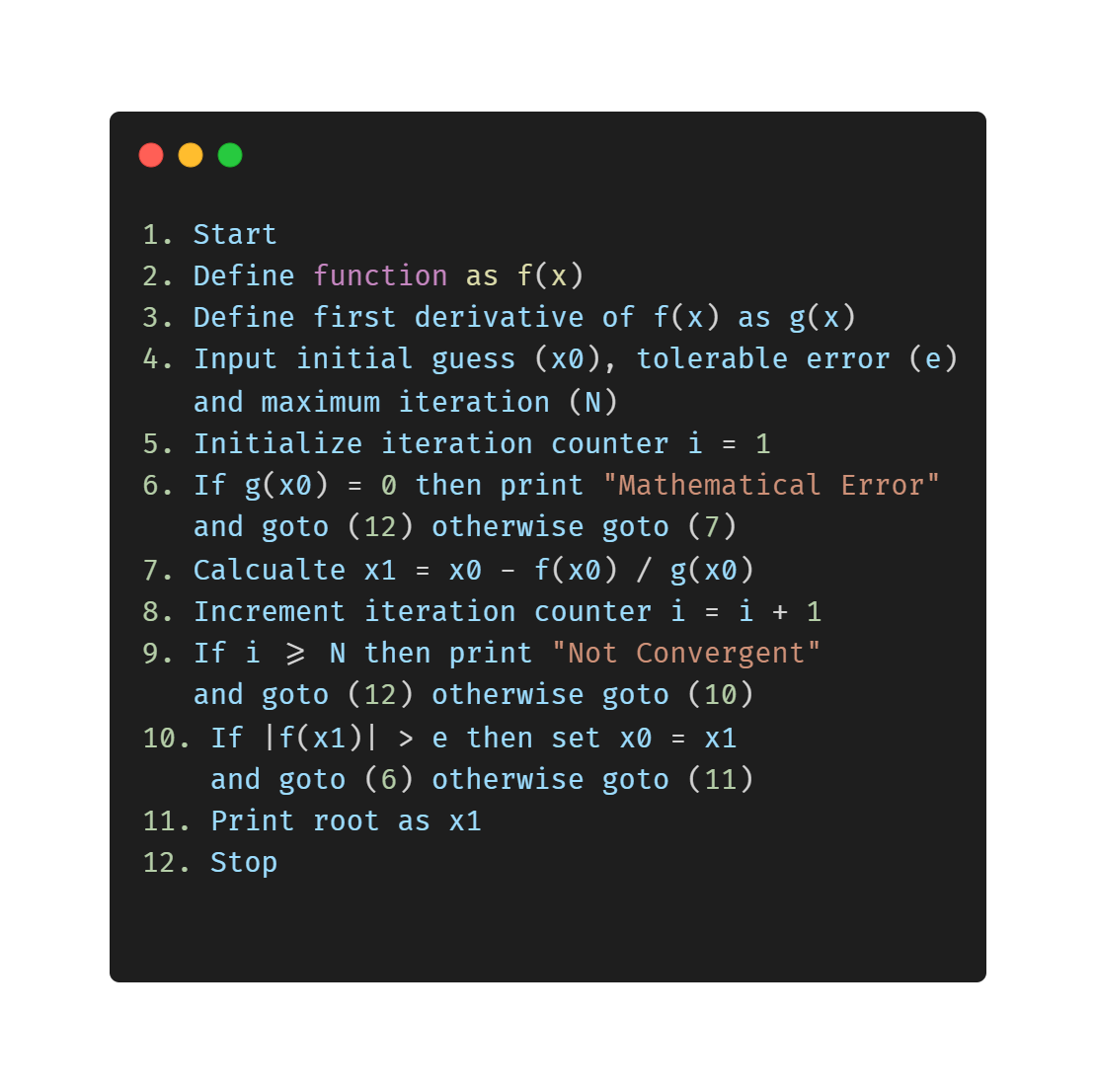
Newton Method
Newton's method is a technique for solving equations of the form f(x)=0 by successive approximation.
The idea is to pick an initial guess x0 such that f(x0) is reasonably close to 0.
We then find the equation of the line tangent to y=f(x) at x=x0 and follow it back to the x axis at a new (and improved!) guess x1.
